Project Sidewalk

Implement Dijkstra's Single-Source Shortest Paths algorithm, reconstruct the shortest paths, and create a command-line program for computing the shortest paths on a graph from a test file.

Learning Objectives

  1. Implement the Dijkstra's shortest path algorithm.
  2. Apply the shortest path concept to real-world accessibility application.
  3. Understand data querying and cleaning.

Introduction

Project Sidewalk is an open-source web-based tool designed to collect street-level accessibility data through crowdsourcing, involving both volunteers and paid workers. Its primary function is to enable users to annotate "street segments" with valuable sidewalk accessibility information, including details about curb ramps, missing or present, obstacles, surface problems, and the absence of sidewalks.

To facilitate easy access to the collected dataset, Project Sidewalk provides an API. This allows users to retrieve the dataset, which consists of Accessibility Scores for streets within a specified region. These scores are determined based on a comprehensive scoring model that takes into account the number of accessibility issues present. The score ranges from 0 to 1, where 0 indicates inadequate accessibility and 1 denotes full accessibility. In the dataset, street segments are represented as a Feature Collection of LineString features, with each LineString having an array of coordinate positions.

For easier data manipulation, the dataset has been extracted into a CSV file. More about this later.

Dijkstra's Shortest Path Algorithm

A graph with nodes and directed edges, visualizing the process of Dijkstra's shortest path algorithm from node A to other nodes, highlighting the the visited nodes and the shortest path found.

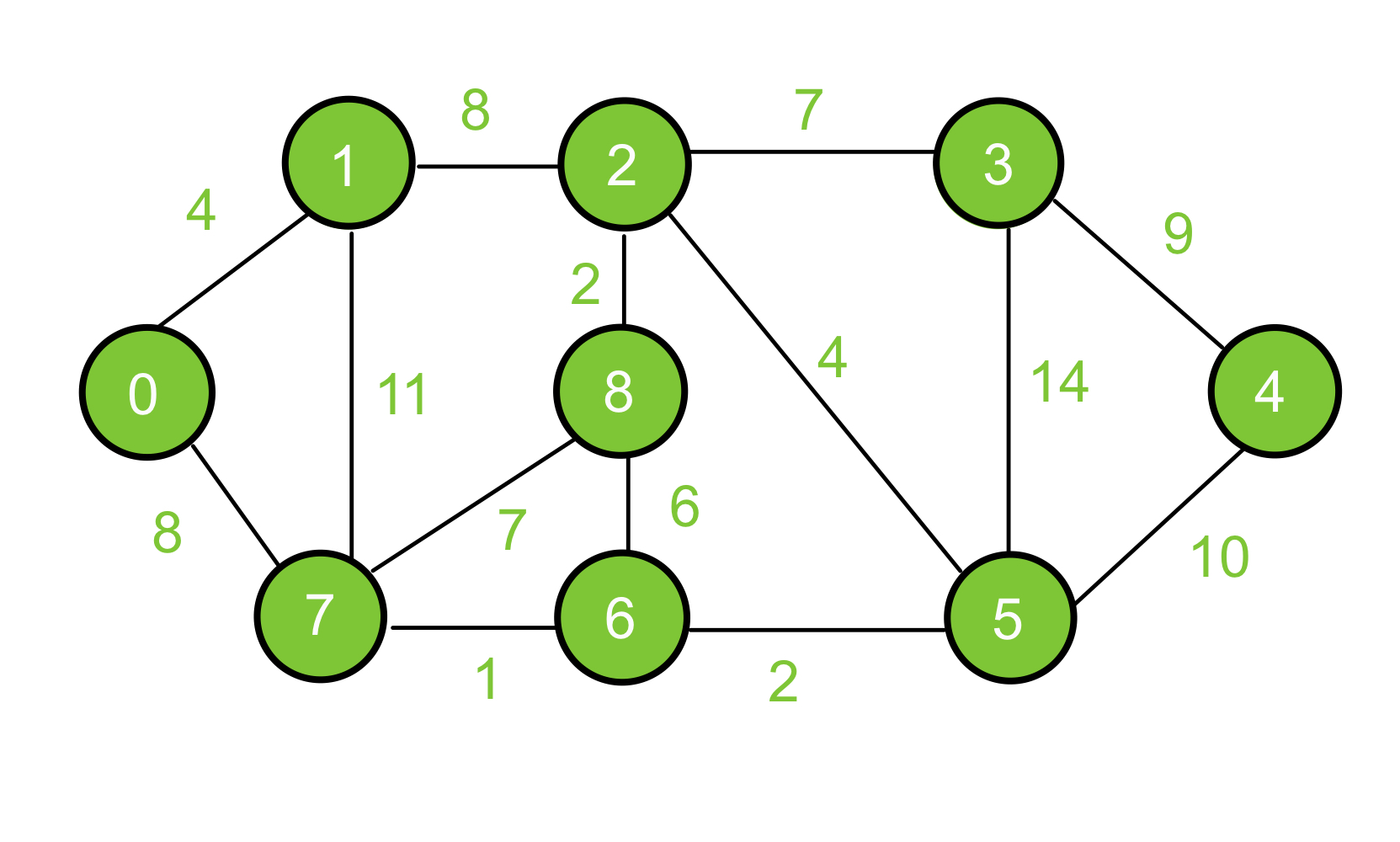
(Figure 1) Dijkstra's Shortest Path Graph.

Dijkstra's shortest path algorithm is a method used to find the shortest path between two nodes in a graph. Imagine you have a map with multiple locations and you want to determine the most efficient way to travel from one location to another. Dijkstra's algorithm helps you find this optimal path by considering the distances between nodes and gradually exploring the graph.

The algorithm starts by assigning a tentative distance value to each node in the graph, with the initial node having a distance of 0 and all other nodes having an initial distance of infinity. Then, it selects the node with the smallest tentative distance and examines its neighboring nodes.

For each neighboring node, the algorithm calculates the total distance from the initial node through the current node. If this calculated distance is smaller than the current tentative distance assigned to the neighboring node, the tentative distance is updated with the smaller value.

The algorithm continues this process, iteratively selecting the node with the smallest tentative distance and exploring its neighbors, updating the tentative distances as necessary, until all nodes in the graph have been visited or the destination node has been reached.

Once the algorithm completes, the shortest path from the initial node to any other node in the graph can be determined by following the sequence of nodes with the smallest tentative distances.

Assignment

In this assignment, your task is to implement Dijkstra's Single-Source Shortest Paths algorithm using a Graph class provided to you. Below is a walkthrough of the six provided classes to get a better understanding of the assignment. Some of these have been completed for you and some of them have skeleton code to help you get started.

1. BasicParser

This class represents a basic parser for sidewalk information. Its purpose is to parse a text file containing street data and create a graph representation of that data. The class follows a specific format where each line represents a street and contains the following information separated by a single space: ORIG, DEST, and DISTANCE. The ORIG and DEST are parsed as Strings, and DISTANCE is parsed as a double. Any content after DISTANCE on each line is ignored. This class has been completed for you.

2. DBParser

This class is a parser specifically designed to parse CSV files for street information. Its purpose is to read a CSV file containing street data and create a graph representation of that data. It utilizes a Scanner class to read the file, maps CSV headers to column indices, and constructs a graph representation of the data by creating 'Sidewalk' objects and adding edges between nodes. Below is an example of what you will find in the given CSV file. This class has been completed for you.

origin dest distance
-122.31013347.6164493 -122.309500947.6164515 0.92414182
-122.30614905344747.6172551505485 -122.306157547.617266 0.999841564
-122.305829747.6171284 -122.305966447.6171369 0.999841564
-122.290208947.6250006 -122.290107947.6250004 0.268941421
-122.289557147.6249996 -122.289234947.6249969 0.5
-122.293130747.6249564 -122.292563547.6249587 0.817574476
-122293717847624721 -122.293668447.6247664 0.377540669
-12229621446247604762281865920700 -122.296195747.6228314 0.97702263
-122.29668147.6225018 -122.29630647.6227565 0.993307149
-122.297069947.6222777 -122.29668147.6225018 0.851952802

3. Graph

This class represents a graph data structure. It allows for the creation of nodes. addition of edges, retrieval of nodes and their neighbors, and reporting of graph statistics. The graph is implemented using an adjacency-list style format, where each node maintains a list of its neighbors. This class has been completed for you.

4. GraphParser

This class serves as a blueprint for creating specific graph parsers by defining the required methods for opening a file a parsing its contents into a graph representation. By extending this class and implementing the 'open()' and 'parse()' methods, you can create parsers for different file formats and customize the parsing logic according to their needs.

5. Node

This class is used in the adjacency-list representation of a graph. It defines a node in a graph with a unique identifier and stores its neighboring nodes along with the weights of the edges connecting them. This class has been completed for you.

6. ShortestPaths

This class provides an implementation of Dijkstra's Single-Source Shortest Paths algorithm. It allows computing the shortest path from a given node to all other nodes in a graph and provides methods to retrieve the shortest path length and path itself. This code includes several TODO comments that indicate tasks to be completed:

  1. Implement Dijkstra's algorithm to fill the paths HashMap with the shortest-path data for each node reachable from the origin. Dijkstra's algorithm is used to find the shortest paths in a weighted graph.
  2. Implement the shortestPathLength method to fetch the shortest path length from the paths data computed earlier.
  3. Implement the shortestPath method to reconstruct the sequence of nodes along the shortest path from the origin to the specified destination using the paths data computed earlier.
  4. Create a ShortestPaths object and use it to compute the shortest paths data from the origin node by origCode.
  5. This TODO is located inside the main method and if destCode was not given as a command line argument, it needs to print each reachable node followed by the length of the shortest path to it from the origin.
  6. This TODO is also located inside the main method and if destCode was given as a command line argument, it should print the nodes in the path from origCode and destCode, followed by the total path length. If no path exists, print a message indicating that no path is found.

Advice

  • You should test your code using both the JUnit test cases provided and the command line program implemented in the main method.
  • Three simple graphs (Simple0.txt, Simple1.txt, Simple2.txt) are provided. Run the algorithm by hand to determine the correct answers for these graphs and verify that your implementation arrives at the correct paths and path lengths.
  • The sample graphs given are not sufficient to test you algorithm's correctness. It's your responsibility to write tests that cover all possible cases that the algorithm could encounter.
  • Make sure your algorithm handles edge cases correctly, including behaving as specified when the destination node is unreachable. Test this using the simplest possible test cases
    • For example, this edge case could be tested using a two-node graph with only an edge from destination to origin.
  • The BasicParser class parses a simple edge list from a text file, such as Simple1.txt and Simple2.txt. The DBParser class parses a CSV file, such as DBCrop.csv. Feel free to write and test using additional graph files in these formats. You may get more CSV files from the Sidewalk API. You provide lat/lng bounds for the ares that you want to query.
  • Some cleaning will be needed for the new CSV files.
    1. Split the coordinates in the "coordinates" column to extract "origin" and "destination". Consider the first coordinate as the "origin", the second coordinate as the "destination", and ignore any extra coordinates.
    2. Rename the column headers accordingly. The below steps will be useful:
      1. Select the cell or column that contains the text you want to split
      2. Select Data > Text to Columns
      3. In the Convert Text to Columns Wizard, select Delimited > Next
      4. Select the Delimiters for your data. Use ')' as a delimiter
      5. Select Next
      6. Select the Destination in your worksheet which is where you want the split data to appear
    3. Select the accessibility attribute you want to consider as the "distance" for your shortest path algorithm.
    4. Rename your selected column as "distance". In the CSV sample file given to you, "distance" is considered to be the access score.

Project Plan and Reflection

Each person must write both a project plan named plan.txt and a reflection named reflection.txt. plan.txt must be completed before the start of the project and reflection.txt must be completed before submitting your project.

plan.txt should include the following information:

  1. A one paragraph summary of the program in your own words. What is being asked of you? What will you implement in this assignment?
  2. In 2-3 sentences, explain your thoughts on what you anticipate being the most challenging aspect(s) of the assignment.
  3. A proposed schedule for when you will work on this assignment with your partner and where you will meet.
  4. A list of at least 3 different resources you plan to use if you get stuck on something.

reflection.txt should include the following information:

  1. Declare/discuss any aspects of your code that are not working. What are your intuitions about why they are not working? Acknowledge and discuss any parts of the program that appear to be inefficient.
  2. What are some of the most important lessons you learned while working on this assignment? Why do you think so?
  3. What was the most challenging aspect of this assignment? Why?

Copyright © 2023